Cash flow duration of actuarial liabilities: What is duration and what can it tell us about actuarial liabilities?
1. Deconstructing actuarial liability
Retirement actuaries calculate liabilities by taking a stream of benefit payments expected to be received from a plan and assigning a measure of current day value to each payment in the stream, expressed as a single cash amount as of a valuation date. Current day value is the concept that money available today has the potential to earn interest. When describing a sum of money to be provided in the future, its value today should be less in order to account for earnings potential. It is the sum of all expected payments, measured at current day value, that defines an actuarial liability. The problems retirement actuaries often work with involve actuarial liability and understanding what happens to that liability when economic forces act on the assumptions used to measure it. In deconstructing actuarial liability, two parts emerge: benefit payments and current day value.
Current day value deconstructs further into interest rates, inflation rates, and yield curves. Interest rates and how their changes affect the measurement of actuarial liability is core to the actuary’s understanding of the risk inherent in retirement liability and in navigating regulatory and accounting landscapes. Interest theory provides a powerful ally to the actuary in the form of duration. The duration of benefit payments expected in a retirement plan provides a framework, as interest rates change, for approximating changes to actuarial liability. To understand how duration is calculated, knowing when and how much cash flows into the hands of retirees is key.
In a retirement plan, the stream of periodic payments being made or expected to be made to a retiree are called cash flows. The measurement of a cash flow’s current day value follows by taking the cash flow and discounting the payment to account for the period between today and the date of payment. For example, suppose an individual age 60 retires from a plan and is guaranteed at age 65 to receive $10,000 annually on his birthday for exactly 15 years. Let’s also assume that payments are certain and would be made to the individual’s estate should the individual predecease the 15th payment. This allows for mortality to be ignored in our example. The chart in Figure 1 is a visual representation of the discounted value of each cash flow. The bars represent the value of each payment as of the retiree’s current age of 60 at an effective interest rate of 4.50%.
Figure 1: Annual Benefit $10,000 Discounted at 4.50% Annually
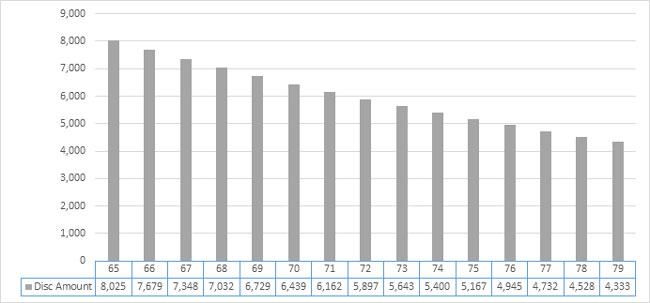
The first gray bar on the left represents the payment at age 65, five years after the valuation age of 60. The discounted amount paid at age 65 as of age 60 is: 10,000 ÷ (1+4.50%)5.
After the discounted value of each $10,000 payment for all 15 years is determined, their sum equals the present value of the cash flow series (actuarial liability): $90,058.
In this article, the reader is introduced to how cash flows and present value are used to calculate duration. The article defines Macaulay duration and Modified duration and discusses how duration is used to approximate the change to actuarial liability resulting from changes in the interest rate used to discount future cash flows. In addition, durations from varying types of plans are compared and errors in the estimates of liability change are used to highlight the topic of convexity. The article concludes by discussing how duration is present in the understanding and applying of more advanced actuarial topics.
2. Duration two ways
Duration is a concept from interest theory used to describe how the present value of a cash flow series changes when small changes are made to the underlying interest rates. Macaulay duration is the weighted average of cash flow timing, where weights are derived from the present value of each cash flow to the total present value. For example, in Figure 1 above, the discounted (disc) amount of the payment at age 65 is $8,025, and the sum of all discounted cash flows is $90,058. The weight of the payment at age 65 is the ratio of $8,025 to $90,058, or 8.91%. This process is followed for each of the 15 discounted amounts in Figure 1 and their sum is 100%. Now average the payment time (1) using the discounted weight (5) you just calculated. This is Macaulay duration. The chart in Figure 2 shows the calculation steps.
Figure 2: Calculation of Macaulay Duration
Interest rate 4.50%
|
(1) Time |
(2) Age |
(3) Amount |
(4) Disc Amount |
(5) = (4) / 90,058 Disc Weight |
(1) X (5) Weighted Time Average |
| 0 | 60 | 0 | 0 | 0.00% | 0.0000 |
| 1 | 61 | 0 | 0 | 0.00% | 0.0000 |
| 2 | 62 | 0 | 0 | 0.00% | 0.0000 |
| 3 | 63 | 0 | 0 | 0.00% | 0.0000 |
| 4 | 64 | 0 | 0 | 0.00% | 0.0000 |
| 5 | 65 | 10,000 | 8,025 | 8.91% | 0.4455 |
| 6 | 66 | 10,000 | 7,679 | 8.53% | 0.5116 |
| 7 | 67 | 10,000 | 7,348 | 8.16% | 0.5712 |
| 8 | 68 | 10,000 | 7,032 | 7.81% | 0.6247 |
| 9 | 69 | 10,000 | 6,729 | 7.47% | 0.6725 |
| 10 | 70 | 10,000 | 6,439 | 7.15% | 0.7150 |
| 11 | 71 | 10,000 | 6,162 | 6.84% | 0.7526 |
| 12 | 72 | 10,000 | 5,897 | 6.55% | 0.7857 |
| 13 | 73 | 10,000 | 5,643 | 6.27% | 0.8145 |
| 14 | 74 | 10,000 | 5,400 | 6.00% | 0.8394 |
| 15 | 75 | 10,000 | 5,167 | 5.74% | 0.8606 |
| 16 | 76 | 10,000 | 4,945 | 5.49% | 0.8785 |
| 17 | 77 | 10,000 | 4,732 | 5.25% | 0.8932 |
| 18 | 78 | 10,000 | 4,528 | 5.03% | 0.9050 |
| 19 | 79 | 10,000 | 4,333 | 4.81% | 0.9142 |
| Sum | 90,058 | 100.00% | 11.18 | ||
| Macaulay duration | 11.18 | ||||
Another derivation of duration is Modified duration. Mathematically speaking, Modified duration is the negative derivative of the present value function with respect to interest rate, divided by the present value. Modified duration is equal to Macaulay duration divided by one plus the interest rate, or following from our example in Figure 2:
(11.18)/((1+4.50%)) = 10.70.
Both Macaulay duration and Modified duration depend on certain interest rate and cash flow assumptions:
- The yield curve is flat, i.e., a single interest rate is used to discount cash flows at all future times.
- Any change in interest rates is a parallel yield curve shift, i.e., changes to the interest rate must be applied equally at all points in time.
- The cash flows do not change as interest rates change, i.e., the expected value of each cash flow is independent of interest rate.
In practice, none of these assumptions will be entirely true, and when using duration to approximate changes in present value, each assumption should be considered in the context of the work being performed. The validity of conclusions drawn from duration should be understood as based on an estimate containing imperfect assumptions. The effects of imperfections in the first two assumptions have been studied but are beyond the scope of this article. The third assumption, while recognized as a significant factor for specific asset classes, is usually a nonissue in the context of payments to retirees in a retirement plan. Typically, retirement plan payments to retirees do not change when the interest rate varies. However, for retirement income plans where retiree payments do change as interest rates vary, proceed with caution when using duration.
3. Measuring the change
The rule of thumb when using duration to approximate change in present value is: Duration represents the percentage change to present value for each 1% change to the interest rate. For example, if the Macaulay duration is 15, every 1% of interest rate movement up or down causes an approximate 15% decrease or increase, respectively, to the present value. Let’s look at our example from above.
Figure 3: Using Duration to Approximate Change
| Change | Interest Rate | Macaulay Duration | Approx. % Change | Present Value |
| 4.50% | 11.18 | 0.00% | 90,058 | |
| -0.50% | 4.00% | 11.18 | 5.59% | 95,092 |
| 0.50% | 5.00% | 11.18 | -5.59% | 85,024 |
When the interest rate decreases or increases by half of 1%, the approximate change is half of the duration. The adjusted present values are then 90,058 times one plus or minus 5.59%.
In our example, changes in the present value due to an interest rate change can be calculated directly without much effort. Regardless of the amount of effort, when changes in present value are calculated directly, the imperfections of the duration estimates can be observed. The chart in Figure 4 shows the observed duration from the direct calculation of present value.
Figure 4: Observed Duration
| Interest Rate | Present Value | Observed Duration |
| 4.50% | 90,058 | n/a |
| 4.00% | 95,040 | 11.07 |
| 5.00% | 85,394 | 10.36 |
Note that the observed duration is greater when the interest rate is lowered half of 1% versus an increase of the same amount. This is typical of retirement liability duration and is evidence of a topic beyond the scope of this article, duration convexity. Convexity is the acknowledgment that change to present value as interest rates change is not a linear function. Instead, the change function has curvature, and using convexity one can improve on the estimates provided by Macaulay duration and Modified duration.
4. Low and slow versus high and fast
When talking about cash flow duration, a comparison between cash flows in different types of plans is necessary. The chart in Figure 5 compares three types of plans: (1) a plan that has been frozen for more than five years, (2) an ongoing open traditional defined benefit (DB) plan, and (3) a plan that pays only a lump sum after termination of employment.
Figure 5: Duration of Differing Plan Type
| Plan Type | Interest Rate | Macaulay Duration | Present Value | Est. Present Value | Est. Error |
| Frozen more than five years | 4.50% | 10.51 | 91,055,849 | n/a | n/a |
| 4.00% | 95,843,672 | 95,840,834 | -0.00296% | ||
| 5.00% | 86,669,791 | 86,270,864 | -0.46028% | ||
| Ongoing traditional DB | 4.50% | 15.01 | 18,027,145 | n/a | n/a |
| 4.00% | 19,401,208 | 19,380,082 | -0.10889% | ||
| 5.00% | 16,804,477 | 16,674,208 | -0.77521% | ||
| Lump sum benefit plan | 4.50% | 6.14 | 1,686,505 | n/a | n/a |
| 4.00% | 1,737,336 | 1,738,281 | 0.05438% | ||
| 5.00% | 1,638,147 | 1,634,729 | -0.20863% | ||
It is not surprising that the largest duration belongs to the ongoing traditional DB plan. An annuity-based plan with a typical distribution of active employees of varying ages who are all eligible for benefits will have higher durations because the younger cohort won’t receive their benefits until later. Plans that pay annuities but don’t have younger active employees eligible for benefits, or plans that only pay lump sums, will have shorter durations. It is generally the case that, when the number of active employees accruing benefits increases, the further out in time are benefits expected to be received, which increases the duration.
Also of note is the error when using duration-derived estimates of present value compared to direct calculation of present value. The error is greater for estimates of change to present value from interest rate increases than from interest rate decreases. This is due to the convexity of duration. When interest rates increase and duration is used to estimate the decrease in present value, Figure 5 shows an overestimation of the decrease in actuarial liability from all three plans. This observation is typical in retirement plans and deserves consideration when providing estimates of actuarial liability using cash flow durations.
5. Duration is not a mystery ingredient
At its core, duration is a weighted average of when benefits are expected to be paid from a plan. Weight is the percentage of total present value that benefits paid at a given future point in time provide. Numerical values of duration can be used to estimate change to actuarial liability due to change in the interest rate. As with any estimate, the results are subject to the constraints and assumptions of the model providing the results. When using duration, cash flows are assumed to remain unaffected by changing interest rates and they are discounted at all future times using the same interest rate.
Once familiar with the basic concepts, duration should be a welcome find when encountered in the practical actuarial problems we attempt to understand and solve. One of the problems actuaries face is the disappearance of DB plans as a result of decreasing interest rates, longevity risk, and increasingly higher market volatility. Implementing a liability-driven investment (LDI) strategy is one way actuaries have taken on this problem, attempting to create an environment sensitive to risks such as interest rate and market volatility. Just like an actuarial liability has a duration, so does an asset portfolio.
One of the ways an LDI strategy achieves a balance between how assets and liability react to external economic forces is by matching their durations. For example, assume liability interest rates are linked to market bond yields, and further assume a retirement plan has a liability duration of 15 with a bond asset portfolio of duration 8. When the bond yield drops, for example 0.25%, the value of the bonds increases and with lower interest rates to discount cash flows, liabilities also increase. Using what we know about duration, we can estimate that the liability will increase by 3.75% and assets will increase by 2.00%. As a result, the funding level of the plan decreases and opportunity presents itself to fix this mismatched response. Using duration, we have opened the door to understanding more about LDI and managing retirement risk. This only scratches the surface of LDI strategies, but it is encouraging to know that next time duration is mentioned, you will have the requisite information to further explore the context in which it is found.
References
1. Alps, R. (2017). Using Duration and Convexity to Approximate Change in Present Value. Education and Examination Committee of the Society of Actuaries Financial Mathematics Study Note, FM-24-17. Retrieved on August 7, 2019, from https://www.soa.org/globalassets/assets/Files/Edu/2017/fm-duration-convexity-present-value.pdf.
2. McCaulay, M. (2013). Duration and Convexity for Pension Liabilities. Society of Actuaries Pension Section News, September 2013 – Issue 81. Retrieved August on 7, 2019, from https://www.soa.org/globalassets/assets/library/newsletters/pension-section-news/2013/september/psn-2013-iss81-mccaulay.pdf.
3. Shang, K. & Hossen, Z. (2019). Liability-Driven Investment, Benchmark Model. Society of Actuaries, Aging and Retirement, April 2019. Retrieved on August 7, 2019, from https://www.soa.org/globalassets/assets/files/resources/research-report/2019/liability-driven-investment.pdf.